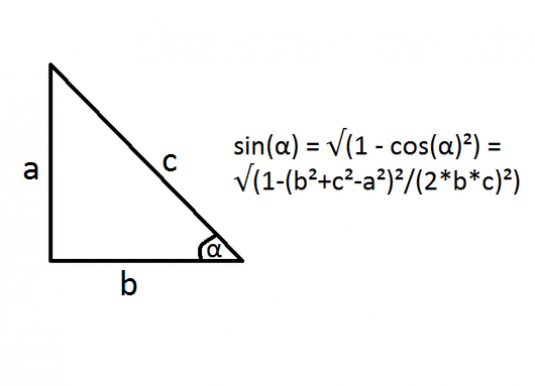Kako pronaći sinus?

Proučavanje geometrije pomaže u razvijanju razmišljanja. Ovaj predmet nužno ulazi u pripremu škole. U životu znanje o ovoj temi može biti korisno - primjerice, pri planiranju stana.

Iz povijesti

U okviru tečaja geometrije također se istražuje trigonometrija, koja istražuje trigonometrijske funkcije. U trigonometrije proučavamo sinuse, kosine, tangente i cotangente u kutu.

Ali za trenutak ćemo početi s najjednostavnijim - sine. Razmotrimo detaljnije prvi koncept - sinus kuta u geometriji. Što je sinus i kako ga pronaći?

Koncept "sinusnog kuta" i sinusoida

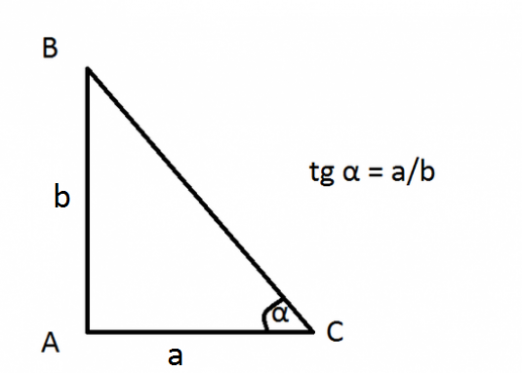
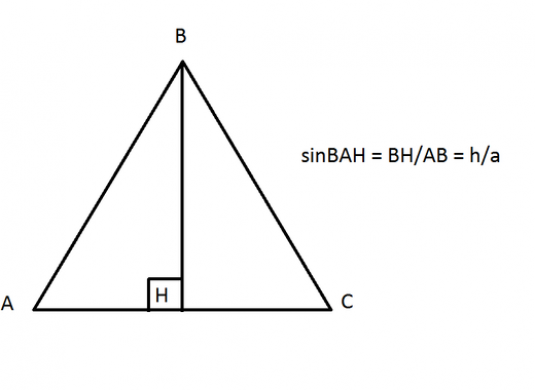
Sine od kuta je omjer vrijednostisuprotna noga i hipotenuza pravokutnog trokuta. Ovo je izravna trigonometrijska funkcija, koja se u slovu označava kao "sin (x)", gdje je (x) kut trokuta.

Na grafikonu, sinus kuta označen je sinusoidom wnjegove osobine. Sinusni val izgleda kao kontinuirana linija vala koja se nalazi u određenom okviru na koordinatnoj ravnini. Funkcija je neparna, stoga je simetrična oko 0 na koordinatnoj ravnini (ostavlja podrijetlo referentne koordinate).

Domena definicije ove funkcije leži uu rasponu od -1 do +1 na kartezijanskom koordinatnom sustavu. Razdoblje funkcije sinusnog kuta je 2 Pi. To znači da se svaki 2 Pi uzorak ponavlja, a sinusni val prolazi punim ciklusom.

Jednadžba sinusoida

• sin x = a / c
• gdje je a katet suprotan kutu trokuta
• c - hipoteza o pravokutnom trokutu

Sinkroni kutovi

1. grijeh (x) = - grijeh (x). Ova značajka pokazuje da je funkcija simetrična, a ako postavimo vrijednosti x i (-x) na obje strane koordinatnog sustava, tada će koordinate ovih točaka biti suprotne. Oni će biti međusobno jednaki.
2. Još jedna značajka ove funkcije je da,da se graf funkcije povećava na intervalu [-Π / 2 + 2 pn]; [P / 2 + 2Пn], gdje je n cijeli broj. Propadanje sinusa kuta promatrat će se na segmentu: [П / 2 + 2 Пn]; [3P / 2 + 2Pn].
3. sin (x)> 0, kada x leži u rasponu (2πn, Π + 2πn)
4. (x) <0, kada je x u rasponu (-P + 2Пn, 2Пn)

Vrijednosti sinusa kuta određene su posebnimtablice. Takve tablice stvorene su kako bi olakšale izračunavanje složenih formula i jednadžbi. Lako je koristiti i sadrži ne samo funkcije grijeh (x), već i vrijednosti drugih funkcija.

Štoviše, tablica standardnih vrijednosti ovihfunkcije uključene su u memorijsku memoriju memorije, kao tablica množenja. To je osobito vrijedno za nastavu s fizičkom i matematičkom pristranosti. U tablici se mogu vidjeti vrijednosti glavnih kutova koji se koriste u trigonometrijom: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 i 360 stupnjeva.

vrijednost kut a (stupnjeva)	0	15	30	45	60	75	90	120	135	150	180	270	360
Vrijednost kuta α u radijanima (u smislu broja pi)	0	π / 12	π / 6	π / 4	π / 3	5/12	π / 2	2/3	3/4	5/6	π	3/2	2π
grijeh (sinus)	0	√3-1 / 2√2	1/2	√2 / 2	√3 / 2	√3 + 1 / 2√2	1	√3 / 2	√2 / 2	1/2	0	-1	0

Tu je i tablica koja definira vrijednostitrigonometrijske funkcije nestandardnih kutova. Pomoću različitih tablica možete lako izračunati sinus, kosinus, tangent i cotangent nekih kutova.

Uz pomoć trigonometrijskih funkcijaJed. Lako je riješiti ove jednadžbe ako znamo jednostavne trigonometrijske identitete i funkcije redukcije, na primjer, kao što su grijeh (n / 2 + x) = cos (x) i drugi. Za takve duhove također je izrađen odvojeni stol.

Kako pronaći sinus kuta

Kada zadatak je pronaći sinus kuta, a pod uvjetom da imamo samo kosinus, tangens ili kotangens kuta, lako možemo izračunati potrebnu pomoću trigonometrijske identitete.

• grijeh²x + cos²x = 1

Na temelju ove jednadžbe možemo pronaći i sinus i kosinus, ovisno o tome koja je vrijednost nepoznata. Dobivamo trigonometrijsku jednadžbu s jednim nepoznatim:

• grijeh²x = 1 - cos²x
• sin x = ± √ 1 - cos²x
• CTG²x + 1 = 1 / sin²x

Iz te jednadžbe možete pronaći vrijednost sinusa, znajući vrijednost kut cotangenta. Za jednostavnost zamijenite grijeh²x = y, a zatim dobivate jednostavnu jednadžbu. Na primjer, vrijednost cotangenta je 1, a zatim:

• 1 + 1 = 1 / y
• 2 = 1 / y
• 2y = 1
• y = 1/2

Sada obavite obrnutu zamjenu igre:

• grijeh²x = ½
• sin x = 1 / √2

Budući da smo uzeli cotangensku vrijednost za standardni kut (45⁰), dobivene vrijednosti mogu se provjeriti iz tablice.

Ako vam se daje vrijednost tangente, i trebate pronaći sinus, drugi će trigonometrijski identitet pomoći:

• tg x * ctg x = 1

Iz toga proizlazi da:

• ctg x = 1 / tg x

Da bi pronašli sine od nestandardnog kuta, na primjer 240⁰, potrebno je koristiti formule za smanjenje kutova. Znamo da π odgovara 180⁰, Dakle, izražavamo svoju jednakost pomoću standardnih kutova raspadanjem.

• 240⁰ = 180⁰ + 60⁰

Trebamo pronaći sljedeće: grijeh (180⁰ + 60⁰). U trigonometrije postoje formule redukcije, koje su u ovom slučaju korisne. Ovo je formula:

• grijeh (π + x) = - grijeh (x)

Dakle, sinus kut od 240 stupnjeva jednak je:

• grijeh (180⁰ + 60⁰) = - grijeh (60⁰) = - √3 / 2

U našem slučaju, x = 60 i P, odnosno 180 stupnjeva. Vrijednost (-√3 / 2) pronađena je iz tablice vrijednosti funkcija standardnih kutova.

Na taj način se mogu proširiti nestandardni kutovi, na primjer: 210 = 180 + 30.

U udžbenicima i internetu možete susresti mnogeformule za izračunavanje trigonometrijskih jednadžbi - oduzimanje, dodavanje, proizvod i podjela trigonometrijskih funkcija različitih kutova jedni s drugima, uspon na snagu i preobrazba jedne funkcije u drugu uz pomoć jednostavnih identiteta i mnogih drugih operacija.

Za više informacija o sinusima i kosinusima pogledajte:

• Što je sinus
• Kako pronaći sinus ako je kosinus poznat