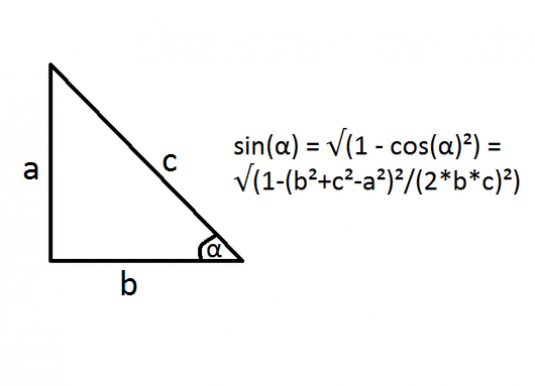Kako pronaći sinus kuta trokuta?

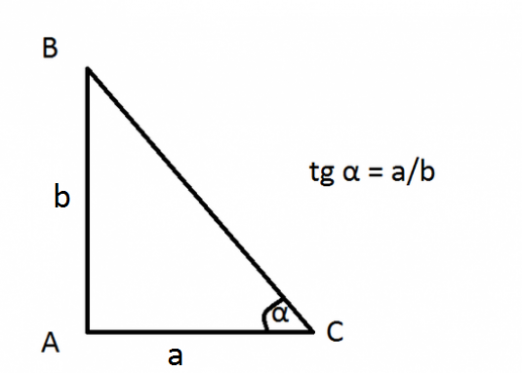
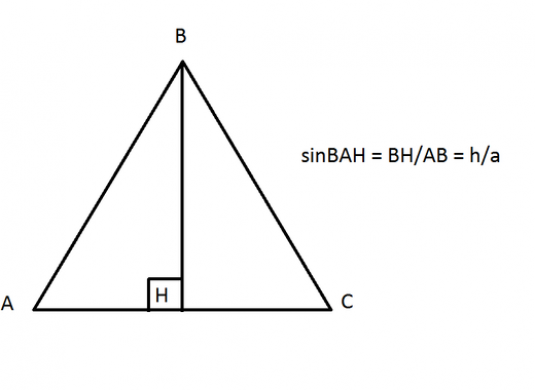
Da biste pronašli sinus kut pravokutnog trokuta, moramo se sjetiti što je sinus po definiciji. A definicija je vrlo jednostavna: sinus je kut jednako omjeru suprotne nogu i hipotenuze.
Kako izračunati sines
Ako imamo trokut ABC, za koji A -pravim kutom, tada će strane AB i AC biti noge, a strana BC - hipotenuzu. Dakle, po definiciji, sinus kut B je jednak omjeru nogu AC na hipotenudu: sinB = AC / BC, a sinus drugog kuta sinC = AB / BC.
U pravokutnom trokutu, funkcije kutovaprikladno je izračunati: nema dodatnih konstrukcija. Dovoljno je znati duljinu desnih strana. No češće je poznat samo dio potrebnih podataka, a ostatak treba tražiti. Razmotrite kako to učiniti.
Tražite sinus s dvije noge
Uzimamo isti trokut ABC s pravim kutom A, u kojem znamo dimenzije nogu: AB = a, AC = c. Za izračunavanje sine kutka C, potrebno je podijeliti katet u hipotenuzu:
- sinC = AB / BC = a / BC (1).
No, hipotenuza će se morati promatrati prema pitagoranskom teoremu:
- BC = √ (AB² + AC²) = √ (a² + b²). (2)
Dajemo pronađenu vrijednost hipotenuze (2) u izrazu (1), dobivamo odgovor:
- sinC = a / √ (a2 + b2).
Tražite sinus na hipotenuzi i susjednoj nozi
Sada, u istom trokutu, moramo pronaći sinus istog kuta C, ali znamo hipoteza BC = b i katoda AC = c. Uz pomoć pitagoreanskog teorema: AB² + AC² = BC² tražimo AB:
- AB = √ (b2-c2).
Sada zamijenite pronađenu vrijednost AB u formuli za sinus:
- sinC = AB / b = √ (b2-c2) / b.
Sinusni izračun na jednoj strani i oštar kut
U trokuta ABC s pravim kutom A, kut B = β je poznat, a kateteza AC = c. Moramo pronaći sinus kuta C.
Metoda 1.
Najjednostavnije - ako se sjetite da je zbroj svih kutova u trokutu 180 °:
- A + B + C = 180 °.
- Kut A = 90 °, B = p,
- C = 180 ° -90 ° - β = 90 ° - β.
- Stoga sinC = sin (90 ° - β).
Metoda 2.
Ali možete ići na drugi način:
- Sinβ = AC / BC; Sinβ = c / BC. Odavde:
- BC = c / Sinβ.
Iz teorema Pitagore AB2 + AC2 = BC2 nalazimo hipotenuzu:
- AB = √ (BC2-AC2).
Zamjenjujemo poznate vrijednosti:
- AB = √ (s2 / Sin²β-c2) = √ ² (1 / Sin² β-1) = s√ (1 / Sin ²-1).
Stoga nalazimo sinus kuta C:
- (1 / Sin β-1) / s / Sinβ = Sinβ √ (1 / Sin²β-1)
odgovor:
- sinC = Sinβ √ (1 / Sin²β-1).