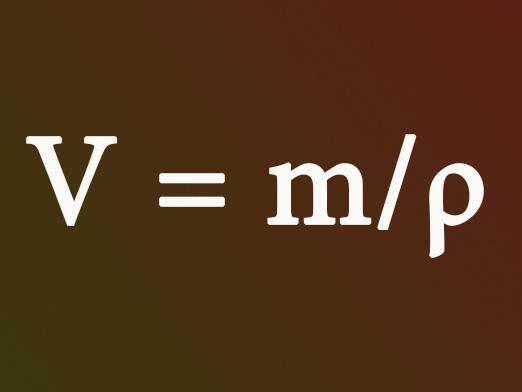Kako pronaći volumen paralelopipeda?

Parallelepiped je posebna varijanta prizma. Njegova jedinstvenost leži u činjenici da se sastoji od lica četverokutnog oblika, a svaki par aviona okrenut jedan prema drugome paralelan je. Postoji nekoliko formula za izračunavanje volumena ove figure: opće, kao i nekoliko jednostavnijih metoda, primjenjive na pojedine slučajeve ovog heksadoga.
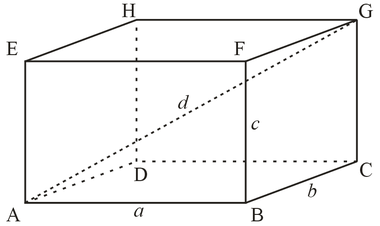
Kako pronaći volumen paralelopipeda? Prvo, morat ćete izračunati područje (S) baze paralelopipeda. Po definiciji, stranice koje leže nasuprot jedna drugoj i oblikuju ovu ravninu su paralelni, kut između njih može biti bilo koji. Prema tome, na površini lica utvrđeno je da je produkt dužine susjednih rubova (a i b) sine kut između njih (α): S = a * b * sin (α).
Zatim umnožite rezultat zaduljina ruba paralelopipeda (c), koja čini kut sa stranama a i b. Od bočne strane, koja je dio ovog rebra ne mora biti okomito na dno na slici, je izračunata vrijednost pomnožiti s sinus kuta nagiba bočne plohe (P): V = S * C * sin (P). Ukratko, formula za izračunavanje volumena paralelopipeda izgledat će ovako: V = a * b * c * sin (α) * sin (β).
primjer:
Na dnu slike, lice s rubovima 15 i 25centimetara, kut između njih je 30 °, bočne plohe ima nagib od 40 ° i duljina rebra od 20 cm Volumen takvih figure biti jednak :. 15 * 25 * 20 * grijeh (30 °) * sin (40 °) ≈ 7500 * 0, 5 * 0,643 ≈ 2411,25 cm3.
Kako pronaći volumen pravokutnog paralelopipeda? U ovom slučaju, formula je uvelike pojednostavljena. Sinus pravokutnog kuta je jednak jedan, svi kutevi ostavljaju formulu, odnosno trebamo samo umnožiti duljinu susjednih rubova paralelopipeda. S duljinom rubova navedenih u prethodnom primjeru, volumen će biti 15 * 25 * 20 = 7500 cm3.