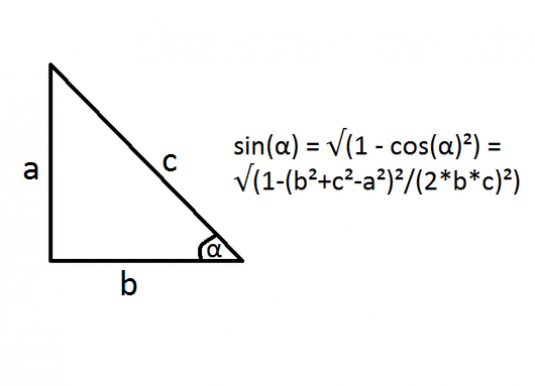Što je sinus?

Tko među nama nije vikao u školi da mu matematikanikad korisno. Svima nam se činilo da sve ove neustrašive formule, teške jednadžbe i složena imena nemaju nikakve veze sa stvarnim životom. No, prije ili kasnije sve znanje koje imamo u školi pronalazi njegovu primjenu. I znajući što sine, kosinus ili tangenta može spasiti vašu reputaciju.

Malo geometrije škole

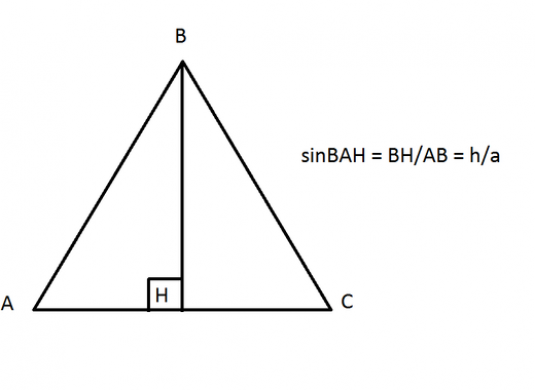
Dakle, sinus je omjer slike u pravokutnom trokutu. Sjetimo se što se sastoji od pravokutnog trokuta.

Uglovima. Zbroj kutova u trokutu iznosi 180^oko, Prednji kut iznosi 90^oko, Stoga, druga dva u zbroju također trebaju dati 90^oko, To jest, imamo jedan pravi kut i dvije oštre.

Stranka. Pravokutni trokut sastoji se od hipotenusa i dvije noge. Dvije noge čine pravi kut, a hipoteza se nalazi nasuprot njoj.

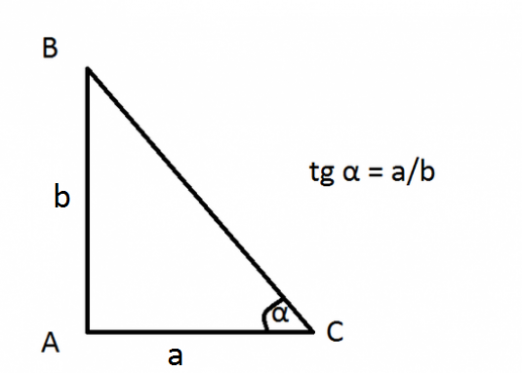
Što je sine od kut? Kao što je već spomenuto, ovaj omjer slike. Ali koje one? Sinus akutnog kuta je omjer nogu, koji se nalazi suprotno ovom kutu, do hipotenuse. Razmotrite primjer:

Sina kutova A je omjer strana a (suprotna noga) na stranu b (hipotenuzu).

Sine kutka C je bočni odnos s (kateta leži nasuprotnom stranom C) na stranu b (hipotenuzu).

To jest, ako su stranice jednake a = 3, c = 4, b = 5, tada će sinusni kut A biti 3/5, a sinusni kut C će biti 4/5.

Što nam to daje? Do sada, ništa, ali pogledajmo još jedan primjer. Povećajmo trokut tako da proširimo strane. Sada smo to učinili:

Kao što se može vidjeti na slici, duljina stranica povećala se, ali uglovi nisu uspjeli. Ali ono što je najzanimljivije - omjer se također nije promijenio!

Pretpostavimo da je d = 6, k = 8, m = 10. Zatim je sinus kuta A d / m = 6/10. Izrežemo ga s dvije strane jednadžbe i dobivamo isti 3/5, kao u prvom slučaju! I bez obzira na to kako promijenite, proširite ili skratite stranke, stav stranaka i dalje će biti isti.

Stoga je jasno da je sinus konstantna vrijednost.

A sada - trigonometrija

Drevni Grci to dugo primijetili. Izračunali su sinusne dijelove glavnih uglova i zabilježili ih kako bi nastavili upotrebljavati već spremne količine, a ne izumiti nove.

Osim sine, kut također ima kosinus(odnos susjedne noge na hipotenuzu), tangenta (omjer suprotne noge na susjednu) i cotangent (omjer susjedne nogu do suprotnog). Sve te veličine nazivaju se trigonometrijske funkcije kuta, a koriste se za izračune i rješavanje problema.

Tajanstveni stolovi Bradys

Svaki put kada ne morate izračunati sinus. Postoje specijalno sastavljeni Bradis stolovi, u kojima su svi sinovi, kosini, tangenti i cotangenti već zabilježeni. Odavde dobivamo informacije. Na primjer, ako znamo kut, znamo njegovu sinus i kosinus. Nasuprot tome, ako je poznat sinus ili kosinus, lako možemo pronaći kut koji se daje.

Naravno, ove trigonometrijske funkcije su ogromne. Sjeti se da je sve jednostavno nemoguće, ali zapravo nije potrebno. Oni uglavnom koriste samo neke od njih.

Malo o kutovima

Ali trigonometrijske funkcije nisu samooštrih i pravokutnih kutova, oni su također za glupo, ali ovdje za njihov nalaz, već će biti potreban krug i graf koordinatnih osi. A ovo je sasvim drugačija priča.

sinusoide

Pogledajmo sada što je sinusoid. Izgleda kao sinusoid ovako:

I jest grafikon sinusne promjene uovisno o promjeni kutova. Kao što je gore spomenuto, strane se mogu mijenjati, a kut ostaje isti - onda će sinus također biti nepromijenjen. No, ako se promijeni kut, tada se omjer slike mijenja, a time i sinusna vrijednost.

Sinusoid prikazuje numeričke promjene u sinusukut i graf je funkcije y = sin (x). Ovdje nije ništa komplicirano, pogotovo jer su vrijednosti sinova svih kutova napisane u Bradysovim stolovima. Ali sjetit ćemo se samo najosnovnijih.

Malo više o označavanju kutova

Svatko zna da se kutovi mjere u stupnjevima iliradijane. Stupnjeve koje mjeri pomoću mjerača, koji izgleda kao polukrug. Jedan stupanj je 1/360 kruga. Zašto? Budući da svaki kut može biti "otvoren" ili "zatvoren". Čak možete otvoriti i za cijeli red i dobiti krug.

Puni promet, kao što je poznato, 360^oko, Ravna crta je kut od 180^oko, To jest, promjer kruga je 180^o. Ili broj Pi. Stoga se ispostavlja da kut može biti 90^oko (u stupnjevima) i Pi / 2 (u radijanima).

Sada pokušajte sjetiti osnovne sinuse. Koji kutovi odmah dolaze u obzir?

Izravni kut - 90^oko, Pi / 2 - sin = 1

Otvoreni kut iznosi 180^oko, Pi - sin = 0

Akutni kut od 60^oko - Pi / 3 - sin = 0,866

Oštar kut 45^oko - Pi / 4 - sin = 0,7071