Kako pronaći polumjer upisanog kruga?

Krug je upisan u graniceredoviti poligon, u slučaju da leži u njemu, dodirujući ravne linije koje prolaze kroz sve strane. Razmotrite kako pronaći središte i polumjer kruga. Središte kružnice bit će točka na kojoj se presijecaju bisectors of angles of poligon. Polumjer je izračunat: R = S / P; S je područje poligona, P je semiperimetar kruga.
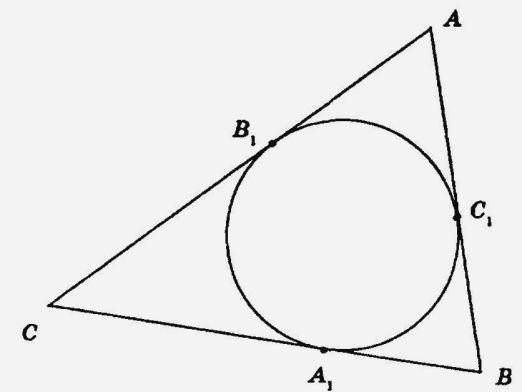
U trokutu
U desnom trokutu upisan je samo jedan krug, središte kojeg se zove centar; Uklanja se sa svih strana istom udaljenostom i predstavlja raskrižje bisectora.
R = (v3 / 6) a - polumjer kruga može se izračunati iz ove formule. U ovom slučaju, a je duljina njezine strane.
U četverokutu
Često moramo odlučiti kako pronaći polumjerupisani krug u ovoj geometrijskoj slici. Mora biti konveksno (ako nema samo-raskrižja). U njemu se može upisati krug samo ako su sume suprotnih strana jednake: AB + CD = BC + AD.
Središte upisane kružnice, sredinadijagonale, nalaze se na jednoj liniji (u skladu s Newtonovim teoremom). Segment, čiji se krajevi nalaze na suprotnim stranama redovne četverokuta, leže na istoj ravnoj liniji, nazvanoj Gaussovom linijom. Središte kruga je točka na kojoj se visine trokuta preklapaju s vrhovima i dijagonalama (Brokarov teorem).
U rombovima
Oni se smatraju paralelogramom s istom duljinom stranica. Polumjer kruga upisan u njemu može se izračunati na nekoliko načina.
- Da biste to ispravno radili, pronađite polumjerupisani krug rombusa, ako je poznato područje dijamanta, duljina njezine strane. Upotrebljava se formula r = S / (2Xa). Na primjer, ako je dijamantno područje veličine 200 mm, duljina stranice je 20 mm, a zatim R = 200 / (2X20), tj. 5 mm.
- Poznat je akutni kut jednog od vrhova. Zatim je potrebno koristiti formula r = v (S * sin (α) / 4). Na primjer, s površinom od 150 mm i poznatim kutom od 25 stupnjeva, R = v (150 * sin (25 °) / 4) ≈ v (150 * 0.423 / 4) ≈ v15.8625 ≈ 3.983 mm.
- Svi kutovi u rombi su jednaki. U tom slučaju polumjer kruga upisanog u rombus bit će jednak polovici duljine jedne strane ove figure. Ako raspravljamo o Euclidu, koji kaže da je zbroj kutova bilo kojeg četverostrana 360 stupnjeva, tada će jedan kut biti jednak 90 stupnjeva; odnosno dobijemo trg.
Sada, nakon što smo pregledali sveformule za izračunavanje radijusa krugova, možete samostalno izračunati bilo koji radijus i dijeliti svoje znanje s prijateljima i poznanicima. Također, ove formule će vam biti korisne u školi kod rješavanja složenih geometrijskih problema. U institutu, ove znniya također neće biti suvišne. Sretno s izračunavanjem radijusa!