Kako pronaći polumjer ograničenog kruga?
Često se u geometriji mora suočitiograničenih krugova i njihovih radijusa. To dovodi do jednostavnog pitanja: kako pronaći polumjer ograničenog kruga? Okruženje opisano oko poligona je krug koji prolazi kroz vrhove tog poligona. Krug je mjesto točaka (geometrijski) u ravnini koja je jednako udaljena od jedne točke ravnine (središta).
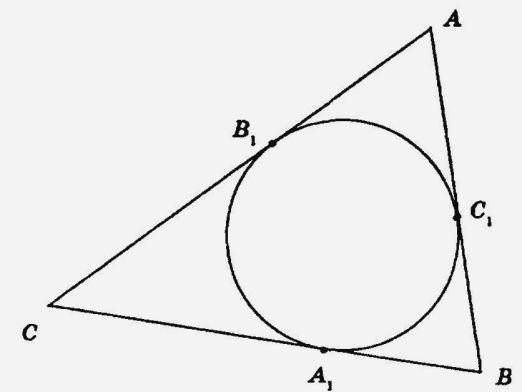
Polumjer ograničenog kruga trokuta
Da biste pronašli polumjer obodnog presjeka trokuta, koristimo jednostavnu formulu za određivanje:
- p = (1/2) (x + y + z), što označavamo s (*)
- R = xyz / (4v (p-z))), što označavamo sa (**), gdje su x, y, z strane trokuta; R je polumjer ograničenog kruga trokuta.
Polumjer ograničenog kruga redovitog poligona
Redoviti poligon je poligon s jednakim stranama i kutovima. A kut između susjednih vrhova redovitog n-gona jednak je:
BOA = x = 360 ° / n, gdje je BOA trokut, x je duljina njezine baze, a n je broj stranica redovnog poligona.
Izrađujemo trokut BOA zasebno. O njemu znamo:
- to je isosceles;
- bokovi trokuta BOA su također radijatori ograničenog kruga redovitog n-gona;
- duljina baze "x" trokuta BOA je strana izvornog redovitog poligona.
- kut između radijusa R, koji smo prethodno izračunali iz formule (**).
Prije svega, potrebno je spustiti visinu do baze i razmotriti pravokutni trokut, koji smo dobili. Pomoću trigonometrijskih funkcija kuta (u ovom slučaju akutne) dobivamo:
grijeh (360 ° / 2n) = x / 2R, iz kojeg dobivamo formulu pravilnog polumjera opisanog kruga redovitog n-gona:
R = x / (2sin (360 ° 2n)), R je polumjer opisanog kruga redovitog n-gona, x je strana regularnog poligona, a n broj redovitih poligona.