Pravila za dodavanje vektora

Da biste izvršili postupak dodavanjavektora, postoji nekoliko načina, koje, ovisno o situaciji i vrsti vektora, mogu biti prikladnije za upotrebu. Pogledajmo pravila za dodavanje vektora:

Pravilo trokuta

Pravilo trokuta je kako slijedi: da bi se dodali dva vektora x, y potrebno je konstruirati vektor x tako da se njegovo podrijetlo podudara s krajnjim vektorom y. Zatim će njihova suma biti vrijednost vektora z, a podrijetlo vektora z će se podudarati s početkom vektora x, a kraj s krajem vektora y.

Pravilo trokuta pomaže ako broj vektora koji se treba zbrojiti nije više od dva.

Pravilo poligona

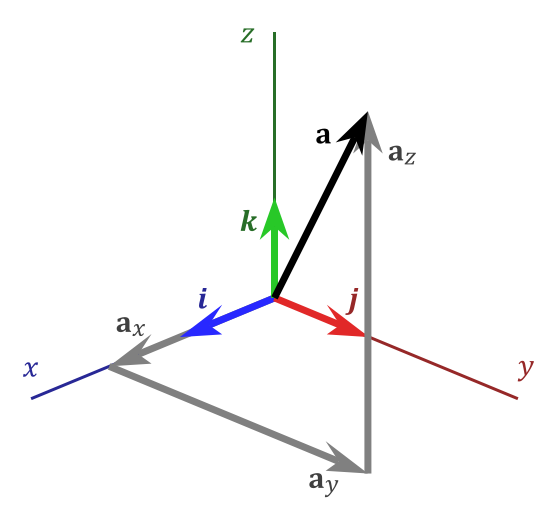
Pravilo poligona je najjednostavnije i najprikladnijedodati bilo koji broj vektora na ravninu ili u prostoru. Bit pravilu je sljedeće: prilikom dodavanja vektora morate ih poredati jedan za drugim tako da se početak sljedećeg vektora podudara s krajnjim prethodnim, a vektor koji zatvara formiranu krivulju je zbroj uvjeta vektora. Ovo je grafički ilustrirano jednadžbom w = x + y + z, pri čemu je vektor zbroj ovih vektora. Nadalje, valja napomenuti da se zbroj ne mijenja od promjena u mjestima uvjeta vektora, tj. (X + y) + z = x + (y + z).

Pravilo paralelograma

Pravilo paralelograma koristi se za dodavanjevektori koji potječu iz jedne točke. Ovo pravilo se navodi da je zbroj vektora xiy, ima početak u jednom trenutku će biti treći vektor Z, podrijetlom također iz ove točke, i gdje su vektori x i y su strane paralelograma, a vektor z - dijagonale. U ovom slučaju, također nije bitno u kojem redoslijedu će biti dodani vektori.

Dakle, poligonsko pravilo, pravilo trokuta i pravilo paralelograma pomažu u rješavanju problema dodavanja vektora apsolutno složenosti, kako na ravnini tako iu prostoru.