Znakovi jednakosti trokuta

Svatko zna da će dva segmenta biti jednaka akonjihove duljine se podudaraju. Ili se krugovi mogu smatrati jednakima ako su njihovi polumjeri jednaki. A koji su znakovi jednakosti trokuta? 7. razred srednje škole: u lekciji geometrije, učenici uče da se, ispada, postoje elementi za koje se jednakost može smatrati jednakima trokutima koji ih sadrže. Vrlo je pogodno za rješavanje problema.
Prvi znak jednakosti trokuta
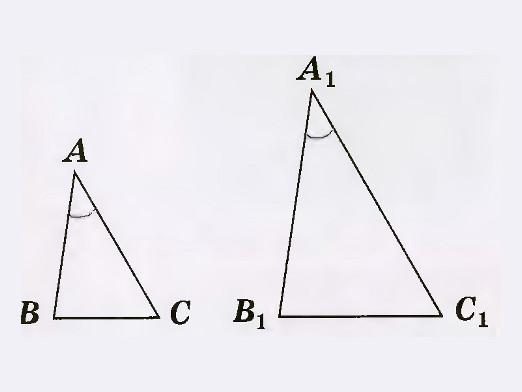
Poštivanje uvjeta odgovarajuće jednakostidvije strane i kut koji je zatvoren između njih u jednom trokutu do dvije strane i kut koji je zatvoren između njih u nekom drugom trokutu, pokazuje da su takvi trokuti jednaki.
Dokaz.
Ako uzmemo u obzir △ ABC i △ A1B1C1, gdje su stranice AB = A1B1, BC = B1C1,
i ∠ABC je jednak ∠ A1B1C1,
tada △ A1B1C1 može biti postavljen na △ ABC na takav način da se A1B1C1 podudara s ABAB. U tom se slučaju trokutovi potpuno podudaraju, jer se svi njihovi vrhovi podudaraju.
(Ako je potrebno, trokut A1B1C1 može se zamijeniti s jednakim "preokrenutim" trokutom, tj. Trokutom simetričnim za A1B1C1.)
Drugi znak jednakosti trokuta
Pod uvjetom da jedna strana i dva uglasusjedni, u jednom trokutu, jednako su jednaki bočnim stranama i dva kutova koji se dodaju u drugom trokutu, tada se takvi trokuti smatraju jednakima.
Dokaz.
Ako su u △ ABC i △ A 1 B 1 C 1 slijedeće jednake vrijednosti
AB = A1B1,
∠BAC = ∠B1A1C1,
∠ABC = ∠A1B1C1.
Postavljamo trokute A1B1C1 i ABC na svaki drugitako da se podudaraju jednake stranice AB i A1B1 i kutovi koji ih prate. Kao u prethodnom primjeru, ako je potrebno, trokut A1B1C1 može se "okrenuti i vratiti". Trokuti podudaraju, pa se stoga mogu smatrati jednakima.
Treći znak jednakosti trokuta
Pod uvjetom da su tri strane jednog trokuta jednaka svim tri strane u nekom drugom trokutu, tada se takvi trokuti smatraju jednakima. Dokaz.
Pretpostavimo da za △ ABC i △ A1B1C1 jednakeA1B1 = AB B1C1 = BC C1A1 = CA Pomakni trokut A1B1C1 na takav način da strana A1B1 poklapa sa stranom AB, a vrhovi B1, a B, A1 i A podudaraju se. Uzimamo krug s središtem A i radijem AC, i drugi krug s središtem B i radijusom BC. Ti se krugovi presijecaju u dvije točke simetrični s obzirom na segment AB: točku C i točku C2. Stoga, C1 nakon prijenosa trokuta A1B1C1 mora se podudarati s obje točke C ili C2. Bilo kako bilo, to će značiti jednakost △ ABC = △ A1B1C1, jer trokuta △ ABC = △ ABC2 jednake (od trokuta su simetrično u odnosu na AB.)
Znakovi jednakosti trokuta pravokutnika
U pravokutnim trokutima, kut između nogu je ravna linija, stoga u bilo kojem pravokutnom trokutu već postoje jednaki kutovi. Dakle, sljedeće primjedbe vrijede.
- Kutni trokuta sukladna ako noge jednog od njih, odnosno jednaka kraka drugoga;
- Kutni trokuta su jednaki, pod uvjetima odgovarajuće kapital hipotenuze i nogama jednog od tih trokuta.
Ako uklonimo iz drugog kriterija, koji govori o ravnopravnosti trokuta, stanje ravnog kuta uz nogu (kao što su pravokutni kutovi u trokutama jednaki) imamo sljedeće:
- takvi trokuta su jednaki, pod uvjetom da je kateti akutna kut susjednog dijela u istom pravokutnog trokuta su jednaki, odnosno za nogu i oštrog ugla, drugi pravokutnog trokuta.
Poznato je da je zbroj unutarnjih kutova trokutauvijek je 180 stupnjeva, a jedan od kutova pravokutnog trokuta je ravna crta. Dakle, ako su u dva pravokutna trokuta oštri kutovi jednaki, tada su preostali kutovi jednaki. Za obične, ne-pravokutne trokuta, kako bi se odredila ravnopravnost figura, dovoljno je znati da su jedna strana i dva kuta jednaka. U pravokutnom trokutu, može se smatrati samo jedan akutni kut i hipotenuzu kako bi se utvrdila ravnopravnost likova.
- Pravokutni trokutići bit će jednaki pod uvjetom da su akutni kutovi i hipotenzija jednog od njih jednaki akutnom kutu i hipotenuzu u drugoj.
Iznenađujuća znanost - geometrija! Znakovi jednakosti trokuta mogu biti korisni ne samo za školske udžbenike, već i za rješavanje svakodnevnih problema koje odrasli rješavaju u svakodnevnom životu.