Kako riješiti granice?

Tijekom matematičke analize,velika količina vremena se dodjeljuje tehnikama proučavanja kako riješiti granice, kako za funkcije tako i za sekvence. Trenutačno postoji niz gotovih metoda i pravila koja, ako se pravilno primjenjuju, mogu pomoći u rješavanju prilično teških zadataka s ograničenjima.

U matematičkoj su analizi uvedeni pojmoviKako riješiti granice funkcija, kao i granice sekvenci. Ako je potrebno izračunati granicu sekvence, zapis ovog primjera izgleda ovako: lim xn = a. Može se vidjeti iz ove sekvence da xn ima tendenciju da. S druge strane, n nastoji beskonačno. Najčešće se sekvence prikazuju kao serija, kao što su, na primjer, p1, p2, p3 ..., pm, ..., pn .... Sve sekvence podijeljene su u dvije skupine: smanjenje sekvenci i povećanje sekvenci.

Kako riješiti granice: formule

Najčešće je količina koja je promjenjiva,na primjer, x ima tendenciju konačnog ograničenja, što je vrijednost a. U ovom slučaju, količina x stalno pristupa vrijednosti a, u kojem vremenu ostaje konstantna. Zapis ove složene definicije vrlo je jednostavan: limx = a. U ovom slučaju, n može imati tendenciju da se beskonačno, i na nulu. Postoje posebne funkcije koje se zovu beskrajne. U njima granica također teži beskonačnosti. Ako se, međutim, smatra druga funkcija koja opisuje usporavanje nečega, tada je smisleno govoriti o granici koja će nestajati.

Sve kapele imaju svoj specifičan skup svojstava. Najčešće, jedna funkcija može imati samo jednu granicu. Ovo je najvažnija i najvažnija vrijednost ograničenja. Sva druga svojstva ograničenja odnose se na njihovu definiciju i rješavanje problema. Također, studenti bi trebali obratiti pozornost na temu kako riješiti granice korijena.

1. Granica suma je jednaka zbroju svih limita: lim (x + y) = lim x + lim y.
2. Granica kvocijenta je jednaka količinu svih limita: lim (x / y) = lim x / lim y.
3. Granica proizvoda jednaka je proizvodu svih ograničenja: lim (xy) = lim x * lim y.
4. Stalni faktor može se uzeti kao granični znak bez gubitka cjelovitosti problema: lim (Cx) = C lim x.

Ako je posao opremljen 1 / x, zakoja teži beskonačnosti, tada će granica ove funkcije biti nula. Ako, međutim, x teži nuli, tada, a granica ove funkcije jednaka je beskonačnosti.

Postoje posebne iznimke od ovih pravilaza trigonometrijske funkcije. Sinusna funkcija x uvijek teži jedinstvu. Kada se ova funkcija približi nuli, sljedeći identitet postaje valjan za nju: lim sin x / x = 1.

Tu su i takvi problemi, gdje jeProces izračuna granica uvodi određenu situaciju, nazvanu nesigurnost. Nesigurnost je situacija u kojoj je izračun granice nemoguć. Jedini način da se riješe takvi problemi jest korištenje pravila L'Hospital. Sve neizvjesnosti su podijeljene u dvije kategorije: nesigurnost oblika nula podijeli se nuli, a također se neizvjesnost oblika beskonačnosti dijeli beskonačno. Ako uzmemo u obzir granicu lim f (x) / l (x), kada f (x0) = 1 (x0) = 0, onda u ovom slučaju eksplicitno pojavljivanje nesigurnosti oblika je nula. Da bi se ovaj problem ispravno riješio, obje se funkcije prvo moraju razlikovati, a zatim se izračunava granica rezultata. Ako uzmemo u obzir nesigurnost nultog stupnja, tada je granica funkcije jednaka lim f (x) / l (x) = lim f (x) / l (x) (za x koji nastoji nuli).

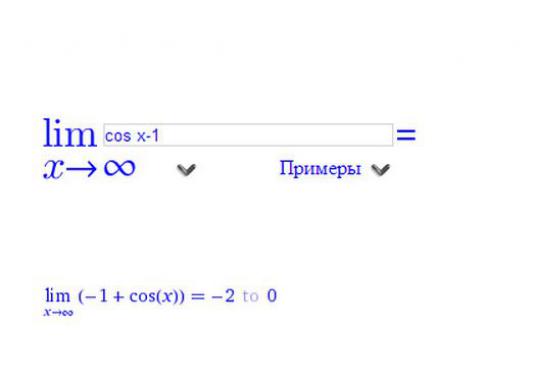
Postoje posebne usluge na kojima možete riješitiograničenje online bilo koje složenosti. Na primjer, web stranica "Calculate Online Limit" nudi standardno ograničenje broja funkcija pomoću posebnog kalkulatora. Ako je potrebno izračunati granicu redoslijeda, bolje je upućivati ​​na ograničenja online kalkulatora na web mjestu "Rješavanje ograničenja na mreži".